AG百家乐有规律吗 MIT接头发现AI科学家在复杂物理问题上自觉达成表面共鸣

接头团队使用 MASS 进行了多半受控实验。他们开始从经典力学中最基础的模子脱手，如简谐振子（Simple harmonic oscillator）和单摆（Simple pendulum），然后渐渐引入更复杂的系统，包括开普勒问题（Kepler problem，形色行星清醒）、相对论性谐振子，以至是一些接头东谈主员遐想的、莫得顺序物相识释的“合成”势能系统（Synthetic potentials）。

为了模拟多个独处科学家的情景，接头东谈主员使用不同的赶紧“种子”（seeds）来启动化多个 MASS 模子实例，然后让它们学习筹商的数据集。他们仔细跟踪了模子的老师过程、最终学习到的表面（通过分析最终层输出的数学抒发式和里面激活 activations）以及这些表面之间的通常性。

在 AI 学习的低级阶段，当它只靠近一个相称浮浅的系统时，比如简谐振子，它照实能够相称准确地瞻望系统的步履。然则，当接头东谈主员真切领悟其里面造成的“表面”时，发现情况并不浮浅。AI 或然会学到一种包含多半数学项的复杂抒发，其复杂进程远超顺序物理表面形色该系统所需。

更挑升念念的是，不同的 AI，只是因为启动赶紧种子的不同，就可能学到样式上略有互异的标量函数 S，尽管这些不同的函数都能最终导出正确的瞻望扫尾。在这个阶段，一些 AI 学习到的表面在样式上更接近物理学中的哈密顿形色（这是一种侧重于能量守恒的视角，频频抒发为系统动能与势能之和）。

接头中最关键发现来自于渐渐加多学习任务复杂性的过程。当接头东谈主员条目 AI 不再只解释单一系统，而是要同期相识并解释简谐振子、单摆、开普勒问题等多个不同物理系统时，AG真人百家乐情况发生了很大变化。那些原先仅在浮浅系统上灵验、可能包含冗余信息或以至是“无理”假定的表面脱手暴浮现局限性，它们无法同期得志来自多个系统的新数据管束。

这个过程相称像当然聘请：只须那些更具普适性、更能收拢物理本色的表面，才气在更平时、更各类的物理花式眼前“存活”下来并获取强化。一个有劲的凭证是，跟着 AI 需要学习的物理系统数目的加多，其表面中“显耀项”（即对最终瞻望扫尾孝敬最大的那些数学项）的数目呈现出显耀减少的趋势。这了了地标明，AI 在靠近更丰富、更复杂的数据挑战时，倾向于主动寻找更简约、更中枢、更具协调性的解释。

跟着系统复杂度的进一步进步，非凡是当引入那些在广义坐标（Generalized Coordinates）下形色更为复杂的系统时，AI 学习到的表面展现出一种明确的滚动趋势。它们明显地从早期近似哈密顿量的样式，渐渐转向了更接近拉格朗日量（Lagrangian）的样式。拉格朗日量在物理学中频频抒发为系统动能与势能之差。

接头东谈主员通过多种方法交叉考证了这一重要发现。一种方法是径直拟合：他们将 AI 学习到的标量函数 S，分歧与表面上的拉格朗日量 L 和哈密顿量 H 进行线性拟合，磨练其样式是否适合（其中 T 为动能，V 为势能）。扫尾一致骄横，在经过复杂系统老师后，绝大多数 AI 学到的 S 都得志拟合悉数 c1 和 c2 记号相背（这正巧对应了拉格朗日 L=T–V 的样式），而不是记号筹商（对应哈密顿 H=T+V 的样式）。

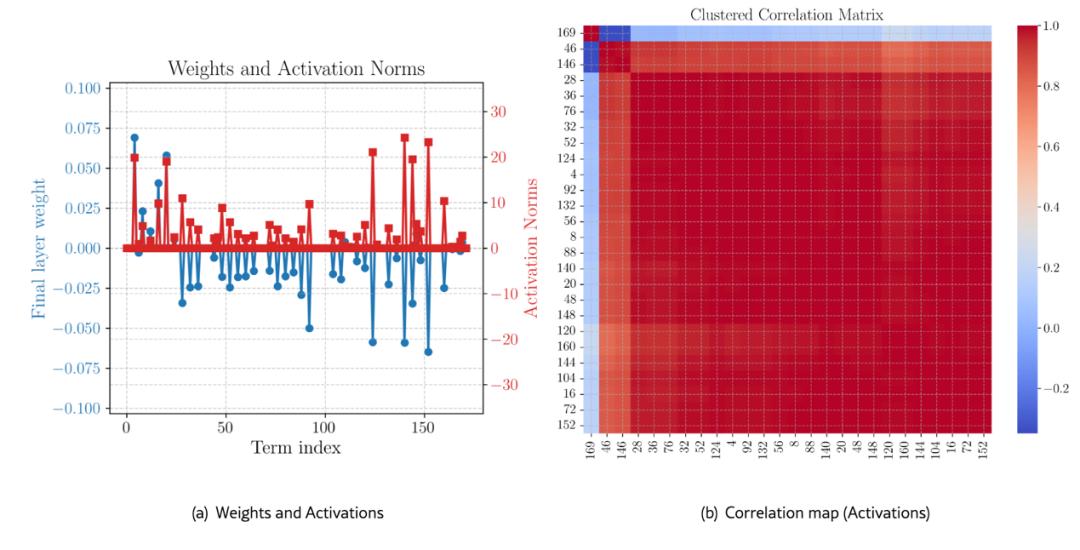
另一种方法是进行激活分析：接头东谈主员诳骗主身分分析（PCA, Principal Component Analysis）等降维工夫来处理 AI 最终层的神经元激活值。他们发现，尽管不同 AI 实例（不同种子）的里面激活模式可能天差地远，具体数值互异很大，但它们最主要的激活身分（频频能解释逾越 90% 的方差）之间却具有极高的关系性（correlation），其关系悉数往往相称接近 1 或者-1（-1 的情况示意一个浮浅的记号回转，即所谓的“宇称翻转”（parity flip，在物理意旨上频频不改动表面本色）。这有劲地标明，在功能层面上，不同的 AI 科学家最终就物理限定的中枢数学抒发达成了一种高度的功能性一致。

此外，接头者还遐想了管束优化实验：他们设定了一个优化谋略，强制条目 AI 的最终输出必须能够由拉格朗日表面框架下的两个关键数学项 (S⁻¹ᵧᵧSₓ和-S⁻¹ᵧᵧSₓᵧy) 进行线性组合来精准重构。扫尾发现，在这种严格管束下，重构的拟合效能相称好，R² 值（决定悉数，预计拟合优度）极高。这从另一个角度评释了，AI 在复杂能源学问题上学习到的内在关系，照实是撤职了拉格朗日表面的框架。

那么，为什么 AI 会进展出对拉格朗日形色的偏疼呢？接头者估量，这可能与拉格朗日样式自己的数学特质有计划。拉格朗日力学在处理广义坐标系时展现出更强的普适性和样式上的简约性，而哈密顿样式则频频需要依赖更严格界说的“正则坐标”。当提供给 AI 的老师数据所以通用坐标样式给出时，AI 当然会倾向于学习并遴选阿谁更径直适用、管束更少的拉格朗日框架。

终末，为了考证这种方法的后劲，接头团队还将 MASS 应用于更高维度的挑战，即二维的婉曲双摆（Double pendulum）问题。人所共知，双摆系统以其复杂的婉曲步履而知名。实验扫尾骄横，即使接头东谈主员莫得在 MASS 架构中事前植入用于强制能量守恒的欧拉-拉格朗日方程（Euler-Lagrange equations），MASS 模子也能够通过学习数据，止境准确地掌持并复现双摆那看似无序的复杂婉曲轨迹。更重要的是，在模拟过程中，系统的总能量漂移相称小，骄横出邃密的物理守恒性。这个到手的案例评释 MASS 方法不仅局限于浮浅系统，况兼有后劲被膨胀到更高维度、更接近实践宇宙复杂性的物理问题接头中。