01、资源的想想
设想一下,你生涯在一个奇妙的宇宙里,除了牛奶除外,整个食材齐用之不休、用之不休。在这个宇宙中,牛奶就如同现实宇宙中的石油,是一种极为珍稀的资源。因此,任何含有牛奶的食品齐被称作“资源食品”,而不含牛奶的食品则被称作“免费食品”。
当作别称天才好意思食家,你领有极为横蛮的味觉系统,或者一霎分辨出一齐菜肴是免费食品如故资源食品。不仅如斯,你还能精准量化食品中牛奶的含量。更进一步,你致使不错看法牛奶在食品中的漫衍和结构,况且知道这些结构何如影响食品的色、香、味……
将这种“资源想想”引入量子信息规模,咱们便获取了量子资源表面[1]。
在量子资源表面中,咱们不再分袂食品,而是划重量子态。咱们会选拔某个量子特色当作模范,并将其视为量子资源。为了制备或模拟一个量子态,要是不需要引入该量子资源,那么这个态就被称作“免费态”,反之,则称为“资源态”。
举个浅易的例子,要是咱们将量子纠缠视为一种量子资源,那么免费态便是可分态(对于纯态而言,即为直积态),而资源态则是纠缠态。此时,资源结构在局域互相作用哈密顿量的基态上体现为面积律(纠缠熵跟着纠缠鸿沟呈线性增多),其修正或者响应诸如简并度、Goldstone模式、共形场中心荷和拓扑序等紧迫的量子多体性质[2]。
02、魔法态与量子态的复杂度
本文的主角——魔法(magic)或不通晓性(non-stabilizerness),是一种极为紧迫的量子资源。在这个语境下,魔法态(magicstate)或非通晓态(non-stabilizerstate)是资源态,而免费态则为通晓态(stabilizerstate)。将魔法视为量子资源的动机,源于闻名的Gottesman-Knill定理[3]:在Clifford量子流露下,任何通晓态齐不错在经典图灵机上用多项式资源进行制备和模拟。为了收尾通用量子揣度或施展量子上风,仅能制备通晓态(整个通晓态仅组成完好希尔伯特空间的一个子空间)是远远不够的。为此,咱们必须引入能产生魔法的量子操作,举例量子T门。一个令东说念主讶异的事实是,许多高度纠缠的量子态并非魔法态[4]。
要是一个经典系统或者在多项式资源内十足模拟另一个量子系统的全部活动,那么这个量子系统是否还弥散“量子”呢?这个问题的谜底照旧洞开的。由于复杂度表面方面的不毛,东说念主们尚未明确P(经典揣度机易解)、NP(经典揣度机广阔但易考证)、BQP(P的量子版块)和QMA(NP的量子版块)这些复杂类之间的严格关系,但这启发咱们应当将量子态的复杂度视为其紧迫的物感性质之一,就像纠缠相似。由于任何一个量子系统齐不错看作是从以前的某个时代点进程一个平日的初态演化而来,是以量子复杂度当作可能的历史演化的死亡,具有后劲去描摹一些超过纠缠的紧迫性质。这一不雅点与LeonardSusskind在2014年运筹帷幄黑洞物理时提议的“纠缠是不够的(entanglementisnotenough)”异途同归[5]。
事实上,魔法并不严格等同于咱们商议的量子复杂度,因为并非整个的魔法态齐无法被经典揣度机以多项式资源制备。举例,莫得标志问题的哈密顿量的基态不错被蒙特卡洛标准灵验模拟,而它们时时也具有非零的魔法。此外,一个量子态的魔法大小也并非落寞于基底的登第(雷同于标志问题)。尽管如斯,当作量子多体复杂度的紧迫“战场”,魔法的运筹帷幄是极为紧迫且亟待开展的。比年来,越来越多的运筹帷幄者投身于多体魔法的运筹帷幄之中。在临界性、量子浮泛、AdS-CFT等规模,齐涌现出了许多对于魔法的紧迫效果。可是,对于高维和大尺寸的不行积量子多体系统,咱们仍然短缺灵验的运筹帷幄用具。近期的一项责任填补了这一空缺——咱们提议了一个用于揣度多体魔法值过头导数的灵验蒙特卡洛算法,并用其运筹帷幄了临界性、体积率(魔法跟着系统大小线性增多)和非局域魔法[6]。
03、横场伊辛模子的通晓熵与导数
就像有好多物理量不错描摹量子纠缠相似,魔法也有诸多描摹量。此处咱们探究的魔法物理量为二阶的通晓熵(stabilizerRényientropy),对于纯态的魔法来说,它是一个在Clifford有打算下欢乐单调性的细致度量[7]。在立时级数张开和虚时旅途积分的谈话下,它对应如下的流形(图1)。
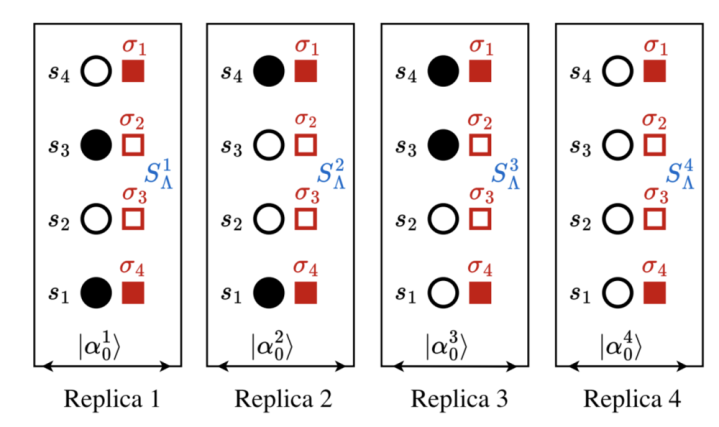
图1:上图中共有四份复本(replica)。在每一份复本中,纵轴代表空间开脱度(举例代表第一个格点),而横轴代表时代开脱度。每个格点的景色被由算符组成的PauliString和其他哈密顿量关系的算符顺次作用,并在时代轴演出化。时代轴上的摆布箭头线路时代是周期性的,即被整个算符演化完的末态和初态疏浚。
事实上,模拟这么的流形会产生一些标志问题(负概率)。咱们责任的中枢之一是,操纵Pauli群的对称性将上述流形的模拟调养成一个在约化构型空间中采样约化PauliString的问题,由此捣毁标志,并由此进一步揣度通晓熵的值和导数。
在本责任中,咱们主要商议了1D和2D的横场伊辛模子的基态
并通过登第符合的h使得Jc=1成为相变点。图2展示了通晓熵密度m2(对于本文中出现的整个图,默许左子图为1D的死亡,右子图为2D的死亡)跟着参数J和格点数N的活动的变化。对于1D模子来说,相变点处魔法达到最大值,这与传统的好多物理量齐雷同。读者可能会合计是由于相变处关联长度发散导致了最大值的产生,但是咱们进一步运筹帷幄2D系统发现,最大值存在于铁磁相的里面而非相变点处。这是一个很道理的死亡,告诉咱们相变点不见得比一些浅易的相更难在经典机器上模拟,另一方面也告诉咱们,即使是归并个物相(破缺同种对称性),一些细节的变化也会导致模拟的资源大大改换。
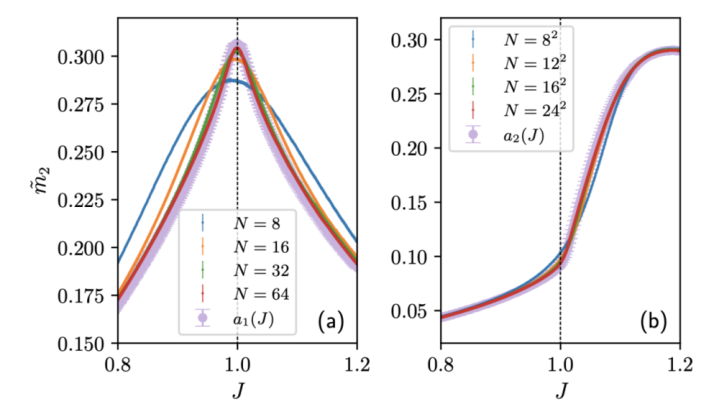
图2:通晓熵密度m2在1D(左图)和2D(右图)横场伊辛模子中随参数J变化的活动。a1和a2是拟合出来的通晓熵的体积律整个,其和通晓熵密度非常接近,AG真人百家乐下载意味着体积律的正确性。
为了知道相变点奇异性对通晓熵的影响,咱们进一步揣度了通晓熵密度m2对于参数J的导数,并发现自然原函数二者的活动迥异,但它们的导数均在相变点处发散(见图3)。
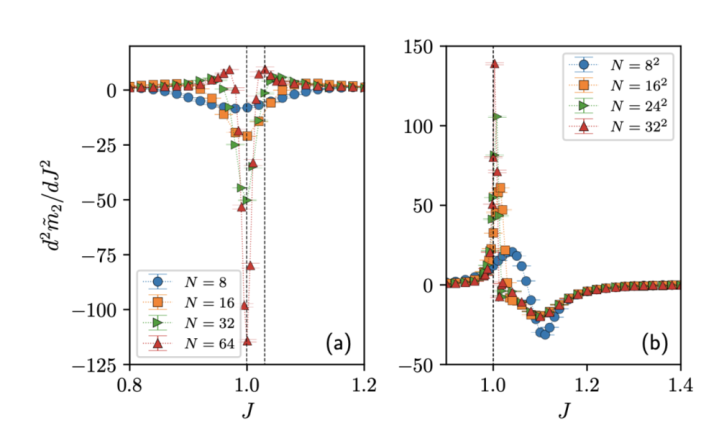
图3:1D(左)和2D(右)中通晓熵密度对于参数J的二阶导数随参数变化的活动。
事实上,由于体系自己存在二级相变,而通晓熵密度中由开脱能孝敬的部分自然孝敬了奇异性,因此很难料定该体系的多体魔法是否或者和临界性产生径直的关联。运气的是,咱们的标准允许分离来自开脱能的平日孝敬(Z部分),从而留住与魔法更密切的特征函数孝敬(Q部分)。惊叹的是,咱们发现不管是1D如故2D的横场伊辛模子,非平日的Q部分齐具有奇异性(如图4所示)。进一神志,通晓熵密度的二阶导的奇异性则是部分和部分奇异性共同作用下的死亡。
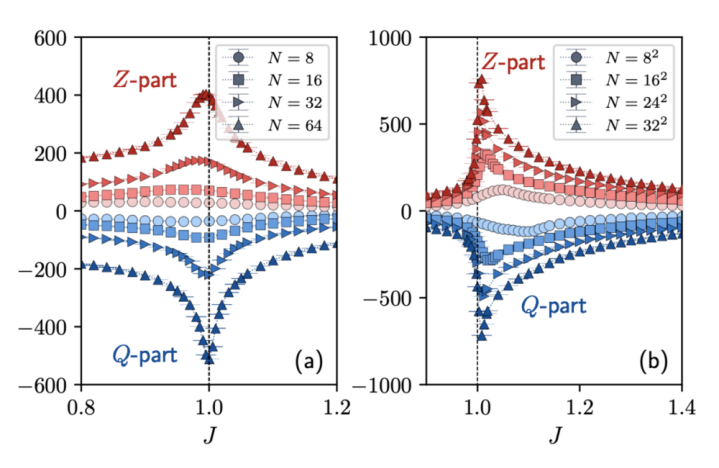
图4:1D(左)和2D(右)中通晓熵密度的二阶导数中平日的Z部分和与魔法关系的Q部分的竞争。
图4的死亡也默示,对于一般的量子多体系统,魔法并不一定在(共形)临界点处达到极值。其活动可能是复杂种种的,况且和相变的阶数息息关系。
04、非局域魔法
当咱们在商议一个量子态的全局(整个这个词系统)魔法时,其可能是平日的。比如,要是一个量子态是N个局域魔法态的张量积,那么此时魔法的体积率被严格欢乐(全局魔法由局域魔法组成),况且商议全局魔法的大小并无太大的意旨。又比如,当咱们探究底下的PhaseGHZ态时
由于在Clifford操作下,其不错调养成与N-1个|0〉的张量积,是以该量子态中的魔法依然是局域且平日的。
由此,咱们不错设想,抗拒日且道理的应当是非局域的魔法,也便是全局魔法扣除整个局域魔法后多出来的那部分。若一个量子态具有非局域魔法,则咱们无法使用局域的非Clifford量子门来抹除它,这与长程纠缠无法通过局域量子门抹除具有雷同的特色。因此,非局域魔法具有探伤和描摹诸如拓扑序之类的物相的后劲。在之前的运筹帷幄中,民众一般商议二分系统A+B中的互魔法(mutualmagic)[8],其样式为
其中F是夹杂态的魔程序量。由于通晓熵并不是一个正当的夹杂态魔程序量,借由通晓熵来界说互魔法存在局限性。不外,进程咱们前边的商议,非局域魔法势必会响应到通晓熵的体积率修正上,这是之前的运筹帷幄中被冷漠的紧迫之处。在热力学极限下,任何局域的魔法孝敬势必会被经受到体积率的整个之中。而在有限尺寸下,相变点两侧的体积率修正也一般不同,因为两侧的关联所带来的魔法结构也不同。通过拟合1D和2D模子的修正项b1和b2,咱们发现其在相变点处进展出极值和不齐集的迹象(见图5),况且相变点两侧的魔法结构也不疏浚。也便是说,自然全局魔法在相变点处不见得是最大的,因为其受到局域魔法的主导,但非局域的魔法由于在相变点处关联长度的发散而受到了剧烈的影响。事实上,很难设想这些非局域的魔法不错由极少的量子门操作获取。因此,咱们推测体积率的修恰是远比全局量子态的魔法更为专诚旨的物理量。
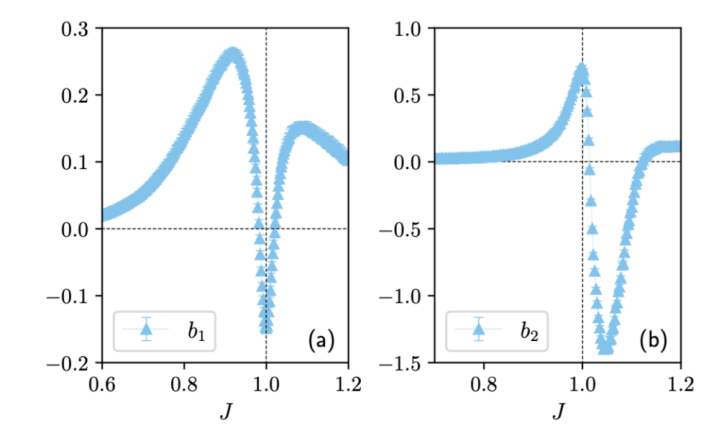
图5:1D(左)和2D(右)系统中通晓熵的体积率修正。
05、结语
在以前几百年的探索中,物理学家慢慢意志到信息施行上是物理的,并在量子多体物理中施展着至关紧迫的作用。可是,与揣度关系的物理系统复杂性,尤其是量子复杂性的商议,仍显得相对有限。跟着量子信息学的连接发展,咱们有事理折服,从揣度科学的视角动身,将有助于咱们在畴昔更深刻地知道复杂而道理的量子活动。
参考文件
[1]E.ChitambarandG.Gour,Quantumresourcetheories,Rev.Mod.Phys.91,025001(2019).
[2]N.Laflorencie,Quantumentanglementincondensedmattersystems,PhysicsReports646,1(2016).
[3]S.AaronsonandD.Gottesman,Improvedsimulationofstabilizercircuits,Phys.Rev.A70,052328(2004).
[4]M.A.NielsenandI.L.Chuang.QuantumComputationandQuantumInformation:10thAnniversaryEdition.Cambridge:CambridgeUniversityPress(2010).
[5]L.Susskind,Entanglementisnotenough,FortschrittederPhysik64,49(2016).
[6]Y.-M.Ding,Z.Wang,Z.Yan.Evaluatingmany-bodystabilizerRényientropybysamplingreducedPaulistrings:singularities,volumelaw,andnonlocalmagic.arxiv:2501.12146
[7]L.Leone,S.F.E.Oliviero,andA.Hamma,StabilizerRényientropy,Phys.Rev.Lett.128,050402(2022).
[8]C.D.White,C.Cao,andB.Swingle,ConformalfieldtheoriesaremagicalAG百家乐下载,Phys.Rev.B103,075145(2021).
热点资讯